배열
배열(array)은 정해진 크기만큼 데이터가 일렬로 저장되는 정적(static) 자료구조다.
각 데이터를 배열의 요소(element)라고 하며 데이터를 가리키는 번호를 인덱스(index)라고 한다.
일반적으로 배열의 인덱스는 0부터 (배열크기) - 1 까지 참조할 수 있다.
접근
배열에서 특정 인덱스의 데이터에 접근하는데 걸리는 시간 복잡도는 O(1)이다.
배열의 첫 번째 데이터에 대한 주소 값에 (데이터 타입의 메모리 크기) X (접근하려는 데이터의 인덱스)를 더하면 되기 때문이다.
즉, 더하기 연산으로 원하는 데이터에 한 번에 접근할 수 있으므로 시간 복잡도는 O(1)이 된다.
검색
배열에서 데이터를 검색하는데 걸리는 시간 복잡도는 O(n)이다.
배열에서 데이터를 검색하면 해당 데이터까지 하나씩 탐색해야 특정 인덱스에 존재한다는 것을 확인할 수 있다.
따라서 마지막 인덱스에 있는 데이터를 검색하는 경우 최대 배열의 크기만큼 연산을 수행해야 하므로 검색의 시간 복잡도는 O(n)이 된다.
삽입
배열에서 특정 위치에 새로운 데이터를 삽입하는데 걸리는 시간 복잡도는 O(n)이다.
크기가 5로 데이터를 5개만 저장할 수 있는 배열에서 인덱스 4에 데이터 1을 추가하려면 추가하려는 위치에 있던 기존 데이터를 뒤로 한 칸 미뤄야 하기 때문에 시간 복잡도는 O(n)이 된다.
단, 배열의 가용 공간보다 배열 크기가 작은 경우엔 (기존 배열의 마지막 인덱스 + 1)로 접근한 후 삽입하면 되므로 O(1)의 시간 복잡도를 갖는다.
삭제
배열에서 특정 인덱스의 데이터를 삭제하는데 걸리는 시간 복잡도는 O(n)이다.
맨 앞의 데이터를 삭제할 경우 배열 전체 데이터를 한 칸씩 앞으로 이동하는 연산을 수행하므로 시간 복잡도는 O(n)이 된다.
단, 삭제하려는 데이터가 마지막 데이터라면 시간 복잡도는 O(1)이 된다.
배열의 마지막 인덱스에 접근해 데이터를 삭제만 하면 되고 위치를 바꿔야 하는 데이터가 없기 때문이다.
연결 리스트
연결 리스트(linked list)는 대표적인 선형 자료구조의 하나로 배열과 달리 크기가 정해져 있지 않은 동적 자료구조다.
이는 연결 리스트가 여러 개의 노드(node)로 구성되기 때문이다.
노드는 데이터와 다음 노드가 저장된 주소 값을 가지고 있다.
연결 리스트는 헤드(head) 포인터와 테일(tail) 포인터로 시작과 끝을 알 수 있다.
연결 리스트에서 첫 번째 노드는 헤드 포인터가 가리키고 마지막 노드는 가리킬 다음 노드가 없기 때문에 다음 노드를 가리키는 주소 값이 NULL이다.
마지막 노드는 테일 포인터가 가리킨다.
이러한 구조는 노드가 메모리에 연속적으로 저장되지 않아도 필요한 연산을 수행할 수 있게 한다.
그래서 연결 리스트에서는 데이터의 추가 및 삭제가 자유롭다.
예를 들어, 연결 리스트에서는 새로운 노드가 추가되어도 기존 노드들의 위치를 변경하지 않아도 되므로 시간면에서 효율적이다.
하지만 연결 리스트는 배열과 달리 인덱스가 없어서 특정 위치의 데이터에 접근하는데 배열보다 시간이 오래 걸린다.
검색
연결 리스트에서 특정 데이터를 검색하는데 드는 시간 복잡도는 O(n)이다.
연결 리스트에서 특정 데이터를 검색하려면 첫번째 노드부터 하나씩 값을 확인하는 선형 탐색을 해야 한다.
추가
연결 리스트에서 데이터를 추가하는 연산 자체는 O(1)이다.
노드를 옮길 필요 없이 이전 노드가 가리키는 노드의 주소 값을 변경하는 작업만 필요하기 때문이다.
하지만 데이터를 추가하려는 위치로 이동하기까지 O(n)이 소요된다.
따라서 연결 리스트의 맨 앞에 데이터를 추가하는 경우에는 O(1)이 소요되고, 나머지 위치에 노드를 추가하는 경우에는 O(n)이 소요된다.
삭제
연결 리스트에서 첫 번째 데이터를 삭제하는 경우 O(1)이 소요된다.
하지만 첫 번째 데이터를 제외한 나머지 위치에서 데이터를 삭제하는 경우에는 해당 위치까지 이동하기 위한 연산을 해서 최대 O(n)이 소요될 수 있다.
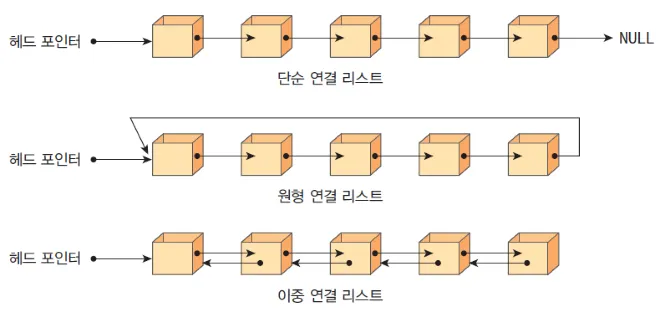
원형 연결 리스트와 이중 연결 리스트
•
원형 연결 리스트
원형 연결 리스트는 마지막 노드가 NULL 값이 아니라 첫 번째 노드의 주소 값을 가리키는 구조다.
다른 연결 리스트와 달리 헤드가 마지막 노드를 가리키면 삽입과 삭제 연산을 효율적으로 수행할 수 있다.
이러한 원형 연결 리스트의 장점은 새로운 노드를 맨 마지막 또는 맨 앞에 삽입할 때 상수 시간이 소요된다는 점이다.
헤드가 마지막 노드를 가리키고 있어서 O(1)에 마지막 노드에 접근할 수 있다.
먼저 마지막 노드가 가리키던 주소 값을 새로운 노드가 가리키게 하고, 마지막 노드는 새로운 노드를 가리키게 한다.
그 다음 헤드가 새로운 노드를 가리키면 마지막에 노드를 추가하는 경우에도 O(1)에 수행을 완료할 수 있다.
또한 순환 구조라서 어느 노드든지 배열의 다른 노드에 모두 접근할 수 있다는 장점이 있다.
•
이중 연결 리스트
이중 연결 리스트에서 노드는 앞 노드의 주소 값과 다음 노드의 주소 값을 모두 저장한다.
그래서 단순 연결 리스트와 달리 양방향 탐색이 가능한 구조다.
단순 연결 리스트보다 구현하기 어렵고, 한 노드당 주소 값 2개를 저장해야 해서 메모리를 많이 차지하는 단점이 있다.
하지만 노드의 연결 순서와 무관하게 노드를 연속적으로 탐색해야 하는 경우에 단순 연결 리스트 대비 시간 면에서 효율적이다.
스택
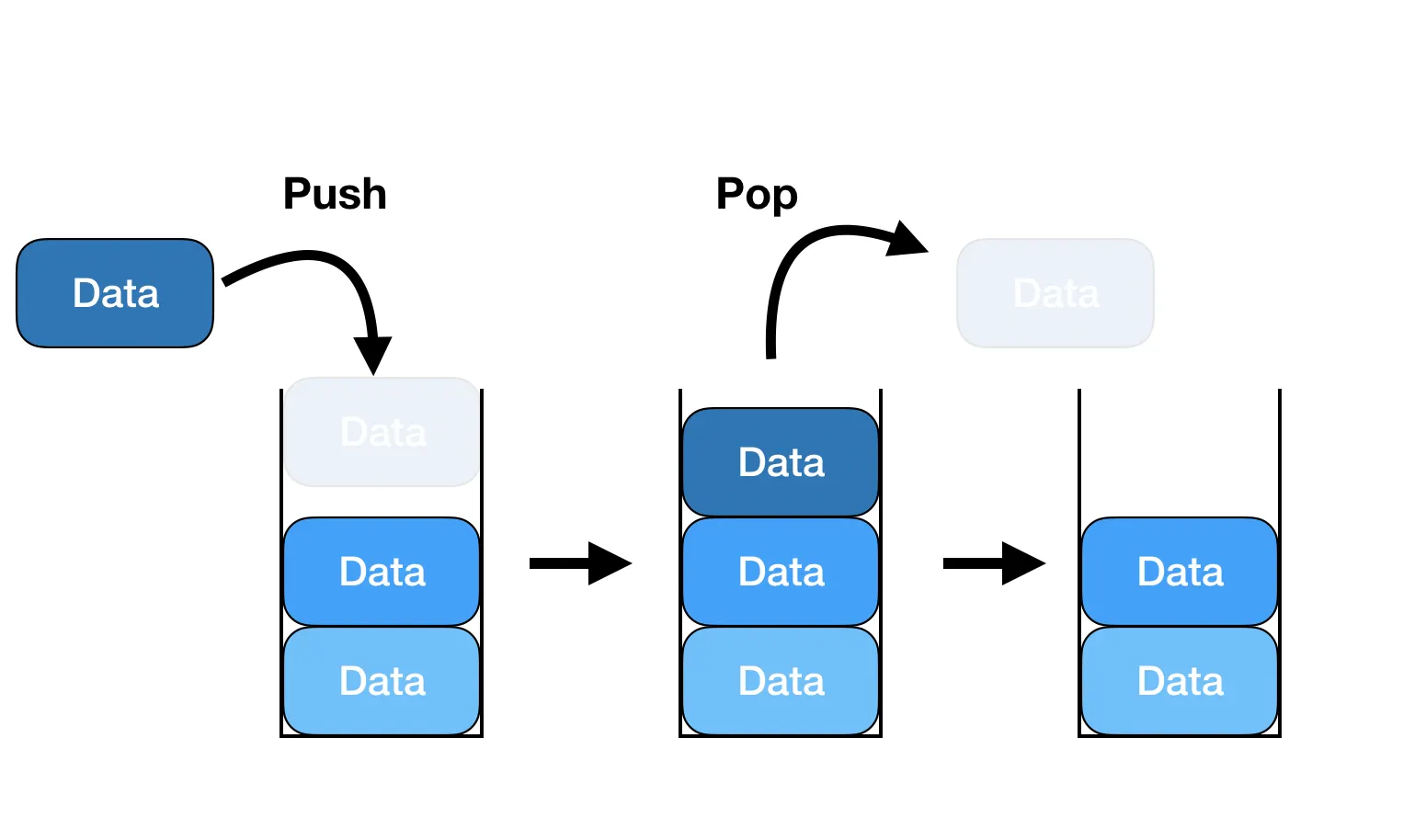
스택(stack)은 데이터를 쌓는 형태로 마지막에 들어온 데이터가 먼저 나가는 LIFO 형태의 자료구조다.
스택에 데이터를 삽입하는 연산을 push라 하고, 스택의 가장 위에 데이터를 저장한다.
스택에 있는 데이터를 삭제하는 연산을 pop이라고 하며, 마지막에 저장한 데이터를 삭제한다.
스택은 top이라는 변수를 이용해 데이터를 마지막으로 저장한 인덱스를 기억한다.
따라서 push나 pop 연산을 할 때 배열을 이용해도 O(1)의 시간 복잡도로 마지막 데이터에 접근할 수 있다.
스택을 구현할 때는 앞에서 설명한 배열과 연결 리스트를 이용한다.
연산 | 설명 | 시간 복잡도 |
push | 스택에 새로운 데이터 삽입 | O(1) |
pop | 스택에서 가장 위에 있는 데이터 삭제 | O(1) |
peek | 스택에서 가장 위에 있는 데이터 확인 | O(1) |
isEmpty | 스택이 비어 있는지 확인 | O(1) |
isFull | 스택이 가득 찼는지 확인 | O(1) |
스택은 주로 어떤 작업의 실행을 취소할 때, 웹 브라우저에서 뒤로가기 할 때 등 최근에 처리한 작업들을 하나씩 꺼낼 때 사용한다.
큐
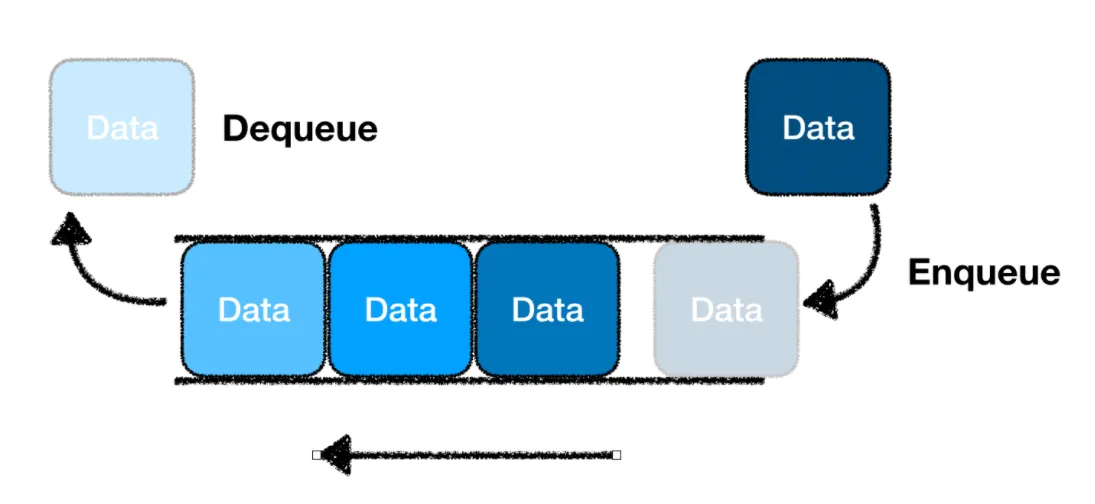
큐(queue)는 데이터가 순차적으로 들어오는 형태로 먼저 들어온 데이터가 먼저 나가는 FIFO 형태의 자료구조다.
큐의 맨 앞을 front, 맨 뒤를 rear라고 하는데, 이를 이용해 큐에서 데이터 삽입과 삭제 연산의 시간 복잡도를 줄일 수 있다.
큐에 데이터를 추가하면 큐의 맨 뒤에 데이터가 삽입되는데 이를 인큐(enqueue)라고 한다.
큐에서 데이터를 삭제하면 큐의 맨 앞에서 삭제되며 이를 디큐(dequeue)라고 한다.
큐도 배열과 연결 리스트를 이용해 구현할 수 있다.
연산 | 설명 | 시간 복잡도 |
enqueue | 큐의 rear에 새로운 데이터 삽입 | O(1) |
dequeue | 큐의 front에서 데이터 삭제 | O(1) |
peek | 큐의 front에 있는 데이터 확인 | O(1) |
isEmpty | 큐가 비어 있는지 확인 | O(1) |
isFull | 큐가 가득 찼는지 확인 | O(1) |
큐를 사용하는 대표적인 예로 운영체제에서 프로세스가 CPU를 할당받기 전까지 대기하는 준비 큐가 있다.
그 외에도 어떠한 작업을 처리할 때 작업 요청이 들어온 순서대로 처리하기 위해 주로 큐를 사용한다.
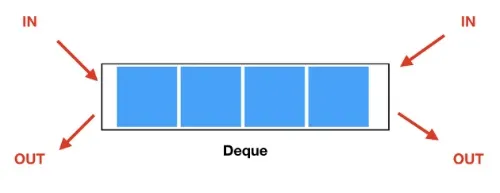
덱(deque)
양쪽 끝에서 데이터의 삽입과 삭제가 모두 가능한 자료구조로 큐와 스택을 합친 형태다.