복잡도와 빅오 표기법
알고리즘을 수행하면 시간과 메모리 공간 등의 자원이 사용된다.
자원을 낭비하지 않으려면 효율적인 알고리즘을 짜는 능력이 필요하다.
알고리즘이 얼마나 효율적인지 정량화하는데 시간 복잡도와 공간 복잡도라는 개념을 사용한다.
시간 복잡도는 알고리즘의 실행 시간을 정량화하는 것이고, 공간 복잡도는 실행하는데 필요한 메모리 사용량을 정량화하는 것이다.
알고리즘의 복잡도는 주로 빅오 표기법으로 나타낸다.
빅오 표기법은 입력 값(n)에 대한 수식에서 최고차항을 기준으로 알고리즘이 수행되는 최악의 시간 복잡도를 표현한다.
최고차항을 기준으로 표현하는 이유는 연산의 수가 극한에 수렴할 때 난머지 항이 복잡도에 미치는 영향은 미미하기 때문이다.
그래서 빅오 표기법은 계수, 상수항은 무시하고 최고차항으로 표현한다.
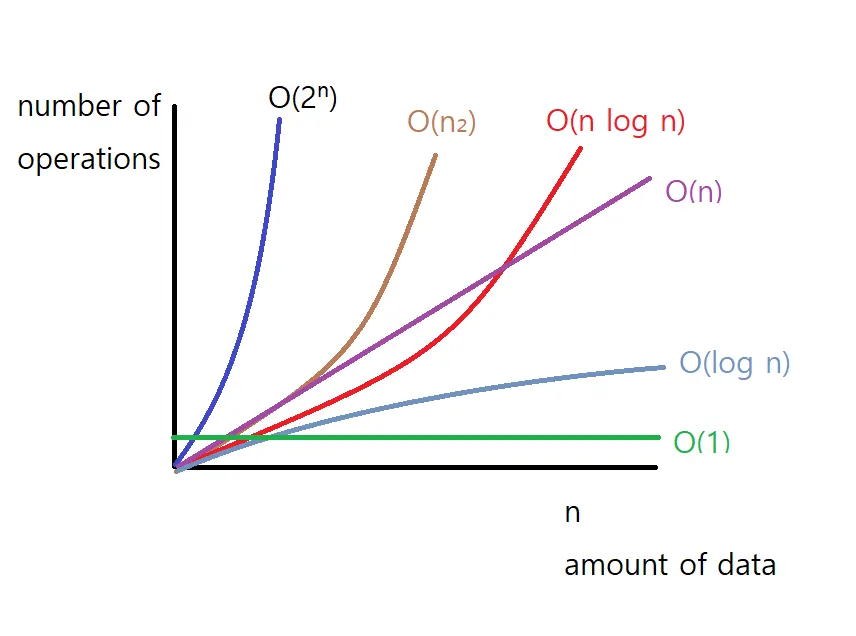
대표적인 빅오 표기법에는 O(1), O(logn), O(n), O(nlogn), O(n^2), O(2^n), O(n!)이 있다.
빅오 표기법에서 입력 값인 n이 극한에 수렴할 때 소요되는 시간의 증가를 그래프로 나타내면 다음 그림과 같다.
그래프를 보면 최고차항이 커질수록 소요되는 시간이 급격히 증가한다는 것을 알 수 있다.
점근적 표기법
알고리즘의 복잡도를 나타낼 때 계수, 상수항 등 중요하지 않은 항목을 무시하고 표현하는 것이다.
•
최악의 경우 : 빅오 표기법
•
평균의 경우 : 빅세타 표기법
•
최선의 경우 : 빅오메가 표기법